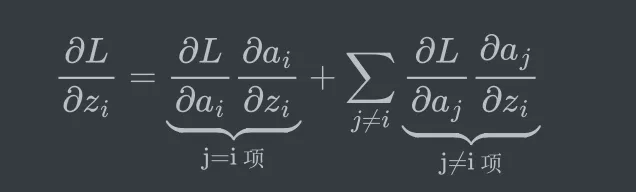在机器学习，尤其是深度学习的分类任务中，交叉熵损失函数（Cross-Entropy Loss）是当之无愧的王者。无论是图像分类、自然语言处理还是其他任何分类场景，你几乎总能看到它的身影。我们都知道，模型通过反向传播（Backpropagation）来学习，而反向传播的核心就是计算损失函数对每个参数的梯度。

作为分类模型中最常用的损失函数，在实际应用过程中，大部分人仅关注如何构造损失函数，很少关注其梯度的计算方式和梯度数量级的问题。本文将详细推导该损失函数的梯度计算方式，之所以进行推导，是为了更好的理解某些时候构造损失函数为何要乘以一个超参数。

交叉熵损失函数梯度计算：

假设我们正在处理一个多分类问题，共有 C 个类别。

模型输出（Logits）: 神经网络最后一层（在激活函数之前）的输出。我们用一个向量 z 表示，

Softmax 激活函数: 将 Logits z 转换为概率分布 a。向量 a的第 j 个元素 a_j 代表模型预测样本属于类别 j 的概率。 公式为：

真实标签（Ground Truth）: 我们使用 One-Hot 编码 来表示真实标签。如果一个样本的真实类别是 i，那么真实标签向量 y 就是一个第 i 位为 1，其余位都为 0 的向量。 例如，如果 C=3，真实类别是第 2 类，则 y = [0, 1, 0]。

交叉熵损失函数（Cross-Entropy Loss）: 用来衡量预测概率 a 和真实标签 y 之间的差距。公式为：

我们的目标是计算损失函数 L 相对于模型 Logits $z_i$ 的偏导数 $∂L / ∂z_i$。

为什么是 z_i？因为 z_i 是由神经网络的权重和偏置直接计算得出的（例如 $z_i = W_i \cdot x + b_i$），求出 ∂L / ∂z_i 后，我们就可以根据链式法则继续向前传播，计算 $∂L / ∂W_i$ 和 $∂L / ∂b_i$，从而更新模型的参数。

应用链式法则：

L 是 a 的函数，而 a 的每一个分量 a_j 都是 z 的所有分量 $z_k$ 的函数。这是一个关键点：改变任何一个 $z_i$ 都会影响到所有的 $a_j$。

根据链式法则，我们可以写出：

现在，我们将这个推导分解成两部分：

1. 计算 ∂L / ∂a_j
2. 计算 ∂a_j / ∂z_i （即 Softmax 函数的导数）

第 1 部分：计算 ∂L / ∂a_j

这部分比较简单。

对 $a_j$ 求偏导，只有当 $k=j$ 时，$log(a_k)$ 项才与 $a_j$ 有关，其余项的导数都为 0。

第 2 部分：计算 $∂a_j / ∂z_i$ (Softmax 的导数)

• 情况 1：i = j (求 $a_i$ 对 $z_i$ 的偏导)

  $$a_i = \frac{e^{z_i}}{\sum_{k=1}^{C} e^{z_k}}$$

  我们使用商的求导法则 $(u/v)' = (u'v - uv') / v²$：

  代入公式：

  $$\begin{aligned} \frac{\partial a_i}{\partial z_i} &= \frac{e^{z_i} (\sum_{k=1}^{C} e^{z_k}) - e^{z_i} (e^{z_i})}{(\sum_{k=1}^{C} e^{z_k})^2} \\ &= \frac{e^{z_i}}{\sum_{k=1}^{C} e^{z_k}} - \left(\frac{e^{z_i}}{\sum_{k=1}^{C} e^{z_k}}\right)^2 \\ &= a_i - a_i^2 \\ &= a_i(1 - a_i) \end{aligned}$$

• 情况 2：i ≠ j (求 $a_j$ 对 $z_i$ 的偏导)

  $$a_j = \frac{e^{z_j}}{\sum_{k=1}^{C} e^{z_k}}$$

  再次使用商的求导法则：

  • $u = e^{z_j}$ => $∂u/∂z_i = 0$ (因为 $i ≠ j$，$e^{z_j}$ 相对于 $z_i$ 是常数)
  • $v = \sum_{k=1}^{C} e^{z_k}$ => $∂v/∂z_i = e^{z_i}$

  代入公式：

  $$\begin{aligned} \frac{\partial a_j}{\partial z_i} &= \frac{0 \cdot (\sum_{k=1}^{C} e^{z_k}) - e^{z_j} (e^{z_i})}{(\sum_{k=1}^{C} e^{z_k})^2} \\ &= - \frac{e^{z_j}}{\sum_{k=1}^{C} e^{z_k}} \cdot \frac{e^{z_i}}{\sum_{k=1}^{C} e^{z_k}} \\ &= -a_j a_i \end{aligned}$$

4. 组合两部分，得出最终结果

现在我们把上面计算出的导数代回到最初的链式法则公式中：

我们将求和项拆分，把 j = i 的那一项单独拿出来：

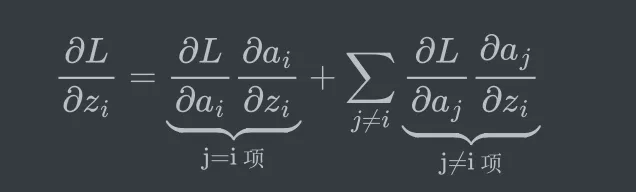
现在代入我们计算好的结果：

• j=i 项: $(-y_i / a_i) * (a_i(1 - a_i)) = -y_i(1 - a_i) = -y_i + y_i a_i$
• j≠i 项: $(-y_j / a_j) * (-a_j a_i) = y_j a_i$

将它们组合起来：

由于 y 是 one-hot 向量，所以 $Σ y_j = 1$。代入上式：

结论

我们得到了非常简洁和直观的最终结果：

这个公式的梯度向量形式为 $∇_z L = a - y$。

课后习题

推导带有温度T的softmax的损失函数梯度。